IARF and the Cooper and Jacob Method

Groundwater hydrologists routinely use the pumping test interpretation method of Cooper and Jacob (1946), a straight-line approximation of the Theis (1935) type-curve solution, to estimate the hydraulic properties of nonleaky confined aquifers from drawdown data measured during the period of infinite-acting radial flow (IARF) when drawdown changes linearly with the logarithm of time. One expects to find IARF after the dissipation of early-time phenomena (e.g., wellbore storage) and prior to the advent of late-time effects such as aquifer boundaries.

Consider the well-known Theis solution for a constant-rate pumping test in a nonleaky confined aquifer of infinite extent:

..... (1)

..... (2)

..... (3)

..... (4)

where s is drawdown [L], Q is pumping rate [L³/T], T is transmissivity [L²/T], t is time [T], r is radial distance [L] and S is storage coefficient [-].

The Cooper and Jacob method approximates the Theis well function, w(u), by truncating the infinite series in (4) after the first two terms:

..... (5)

The approximation in (5) assumes that u is small, i.e., t is large and r is small. It is precisely when (5) is valid that infinite-acting radial flow is identified from drawdown data.

How small should u be for (5) to be valid? The threshold for IARF (i.e., when Cooper and Jacob becomes valid) is often given as u ≤ 0.05 (Driscoll 1986) or u ≤ 0.01 (Kruseman and de Ridder 1994); however, we can see for ourselves when (5) is valid by plotting w(u) versus 1/u (dimensionless drawdown versus dimensionless time) on semilog axes and looking for a constant logarithmic derivative plateau (Figure 1).

Figure 1. Theis (1935) solution (blue curve) plotted as w(u) versus 1/u on semilog axes. Logarithmic derivative shown by red curve.

It is evident from Figure 1 that the slope of the drawdown and the value of the derivative are each essentially constant when 1/u ≥ 50. Hence, when u ≤ 0.02, the Cooper and Jacob approximation of the Theis well function is safe to use. Figure 1 demonstrates just how useful derivative analysis can be for the detection of the IARF regime.

Visit Aquifer Testing 101 to learn more about pumping test interpretation with more examples of infinite-acting radial flow.

Follow HydroSOLVE on LinkedIn and Google+!

Infinite-Acting Radial Flow Regime

At the outset of interpreting a pumping test, an important feature to detect in the response data is infinite-acting radial flow. During infinite-acting radial flow, steady pumping in a nonleaky confined aquifer of infinite extent produces late-time drawdown that changes with the logarithm of time since pumping began. Infinite-acting behavior occurs after wellbore storage effects have dissipated and before the influence of aquifer boundaries. One may observe this flow regime by plotting the familiar Theis (1935) solution on semilog axes (Figure 1); at late time, a graph of dimensionless drawdown, w(u), versus dimensionless time, 1/u, plots as a straight line and the logarithmic derivative is constant.

 

Figure 1. Infinite-acting radial flow in a nonleaky confined aquifer illustrated with Theis (1935) solution (dimensionless drawdown and dimensionless derivative shown by blue and red curves, respectively).

This late-time behavior of the Theis model is well known to groundwater hydrologists. The period of infinite-acting radial flow is the basis for the tried-and-true Cooper and Jacob (1946) method which one may use to find the transmissivity and storage coefficient of a nonleaky confined aquifer by matching a straight line to late-time drawdown data from a constant-rate pumping test plotted on semilog axes.

A derivative plot is very useful for detecting the infinite-acting radial flow regime under steady pumping conditions. One starts by looking for a derivative plateau (constant derivative) to tentatively identify infinite-acting radial flow. For example, the response data from a constant-rate pumping test shown in Figure 2 suggest that infinite-acting radial flow conditions are present after approximately 30 minutes of pumping once the derivative stabilizes.

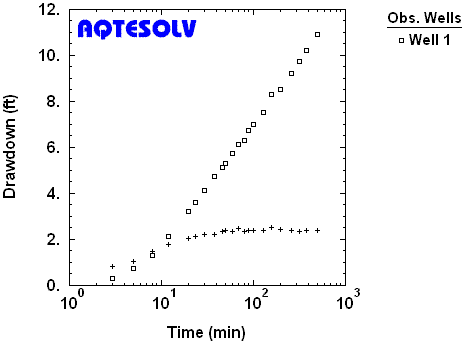Figure 2. Derivative plot of drawdown (squares) and derivative (crosses) measured in an observation well during constant-rate pumping test in a nonleaky confined aquifer (Walton 1962).

Note that the derivative plateau in Figure 2 exhibits some noise; derivative fluctuation at the plateau is common in the application of derivative analysis, but the presence of a near-constant derivative in this example is clear and corresponds to the emergence of a well-defined straight line in the drawdown data.

The foregoing results suggest that the derivative plot is an indispensable tool for aquifer test interpretation; however, the mere existence of a derivative plateau does not immediately confirm infinite-acting radial flow conditions. For example, an aquifer limited by a no-flow boundary can produce a constant derivative that is not diagnostic of the infinite-acting radial flow regime. In such a situation, geologic mapping of lithologic contacts, faults and other low-permeability features would be invaluable in making a correct interpretation.

Visit Aquifer Testing 101 for a catalog of derivative plot signatures with more examples of infinite-acting radial flow in pumping tests.

Follow HydroSOLVE on LinkedIn!